Algorithms

Below are some homework / notes about algorithms.

Merge Sort

def merge_sort(l):
    """ merge sort implementation """
    length = len(l)
    if length in [0, 1]:  # base cases
        return l
    middle = length // 2
    left, right = l[:middle], l[middle:] 
    left_sorted = merge_sort(left)
    right_sorted = merge_sort(right)
    merged = []
    i = j = 0
    while i != len(left_sorted) and j != len(right_sorted):
        if left_sorted[i] < right_sorted[j]:
            merged.append(left_sorted[i])
            i += 1
        elif left_sorted[i] > right_sorted[j]:
            merged.append(right_sorted[j])
            j += 1
        else:
            raise NotImplementedError
    if i != len(left_sorted):
        merged.extend(left_sorted[i:])
    if j != len(right_sorted):
        merged.extend(right_sorted[j:])
    return merged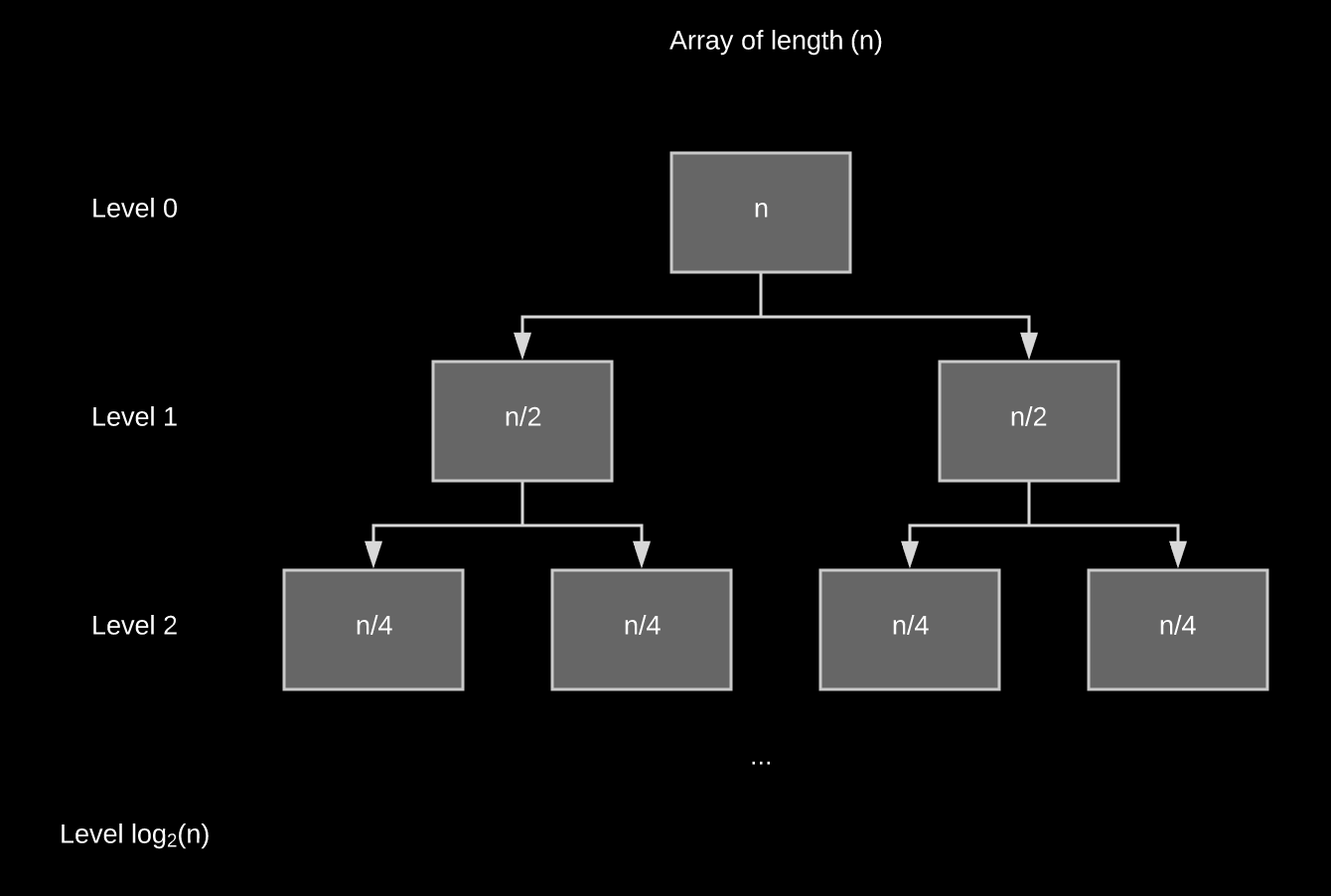

vim

There are $log_2(n) + 1$ number of levels.
At level $j$, we have $2^j$ sub-problems, of size $\frac{n}{2^j}$
Each sub-problem do $x$ operation.
So we have $x \cdot n \cdot log_2(n) + x \cdot n$ operations.
Removing lower order term and leading constant factor: $O(n \cdot log(n))$